|
Найдите все значения параметра 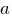 , при каждом из которых система , при каждом из которых система
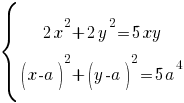
имеет ровно два решения.
Решение.
Посмотрим внимательно на систему. Заметим, что если мы поменяем местами 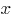 и и 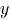 , то система от этого не изменится. Системы такого рода называются симметрическими, и если пара (x;y) является решением симметрической системы, то пара (y;x) также будет решением этой системы. Следовательно, должно быть только одно значение , то система от этого не изменится. Системы такого рода называются симметрическими, и если пара (x;y) является решением симметрической системы, то пара (y;x) также будет решением этой системы. Следовательно, должно быть только одно значение 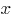 и соответствующее ему значение и соответствующее ему значение 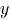 , которые являются решением системы. В этом случае система будет иметь ровно два решения: (x;y) и (y;x) (!) , которые являются решением системы. В этом случае система будет иметь ровно два решения: (x;y) и (y;x) (!)
В первом уравнении отсутствует параметр, и из него мы можем получить соотношение между 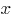 и и 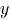 . .
Перенесем 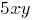 влево. влево.
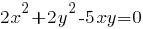
Разделим обе части на 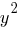 в предположении, что в предположении, что 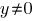 . (Если . (Если 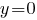 , то , то 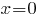 , в этом случае для пары (0,0) мы не можем получить симметричную ей, и не можем получить ровно два решения.) , в этом случае для пары (0,0) мы не можем получить симметричную ей, и не можем получить ровно два решения.)
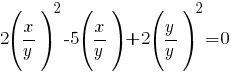
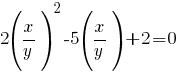
Решим квадратное уравнение относительно 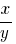 и получим и получим
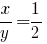 или или 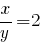
Отсюда 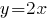 или или 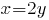
Рассмотрим первый случай: 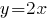 . Подставим . Подставим 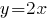 во второе уравнение системы. Получим: во второе уравнение системы. Получим:
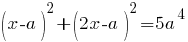
Просматривается квадратное уравнение относительно 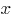 . Нас интересует, при каких значениях . Нас интересует, при каких значениях 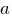 это уравнение имеет единственно решение. (см. (!)) это уравнение имеет единственно решение. (см. (!))
Квадратное уравнение имеет единственное решение, если 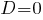
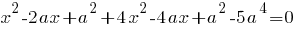
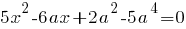
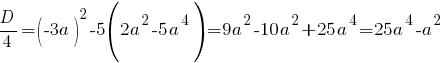
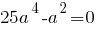
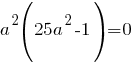
Отсюда:
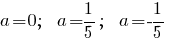
Если 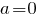 , то , то 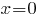 и соответственно и соответственно 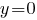 - этот случай нам не подходит. - этот случай нам не подходит.
То есть 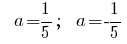
Второй случай: 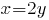 абсолютно аналогичен первому. абсолютно аналогичен первому.
Ответ: 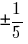
| 

